このページは、水の性質を知ることから、ポンプ室、ホース内部の水の流れる仕組みを理解していきます。
これを分かることで、論理的に水の流れ、摩擦損失及び背圧損失を理解できます。
後輩に説明するときにも少し、賢く見られます。この機会に理解していきましょう。
水の性質

端的に過剰書きで行きます。このサイトでも多く利用している知識をまとめて書いていきます。
- 固体(氷)、液体(水)、気体(水蒸気)の形態がある
- 0℃以下になれば氷になり、100℃以上になれば水蒸気となる
- 水蒸気の体積膨張は1700倍になる
- 比熱効果が低く、温まりにくく、冷めにくい
- 熱量の吸収率が大きく、水蒸気の体積膨張に伴う酸素濃度を減らすことができるため、最良の消火手段として活用されている
- 密度は1㎥で1,000kg
- 非圧縮性物質(詳しくはこのページ)外部から力を加えても形が変わりにくい
- 粘性は比較的に低い※
※粘性とは、液体が持つ粘りみたいなもの。水飴と水では粘りは水飴の方がありますね。でも、水にも少し粘りがありまうすので、それがホース内部を流れる流体になるときに摩擦損失と大きく関係してきます。
圧力
圧力は押している面積と力が関係します。ここでは液体における深さの下向きに掛かる圧力(背圧)関して説明します。

が成り立ちます。
この式では、液面からの深さを測れば、その圧力を求めることができます。
流体が水の場合、密度が1,000(kg/㎥)、重力加速度9.8を当てはめると
圧力(Pa)=1,000 (kg/㎥) × 9.8 × 高さ (m)
=9,800 × 高さ (Pa)
=0.098 × 高さ (MPa)
≒0.01 × 高さ (MPa)
となります。つまり、水は1mの高さに付き、底部では0.01MPaの圧力が掛かります。
消防ポンプでの背圧がこれにあたり、10mで0.1MPaの圧力損失が発生することが理論上分かります。(大気圧は無視してます。)
※10 × 10 × 10 × 10 × 10 × 10 Pa = 1MPa
圧力換算
| 単位の名称 | 単位 | 換算 |
| パスカル | Pa | 1Pa=1N/㎡ |
| 重量キログラム | kgf/c㎡ | 1kgf/c㎡=0.09806MPa ≒0.1MPa |
パスカルは、ポンプでよく使う圧力ですね。重量キログラムは空気呼吸器ではこの表示をしているものもあると思います。単位換算による計算は覚えていても損はないでしょう。
水の流れ(流体)

ホース内部や管を通る水の流れには必ず、前述した粘性の作用が働き、それは摩擦損失として表されます。
例えば、ホースであれば、内装に触れている部分の流れる速度(流速)は0になり、中心の部分が最大の速度で流れます。
この単位時間に流れる流束を流体(体積:3次元)で表したときの量を流量といいます。
2次元図

3次元図
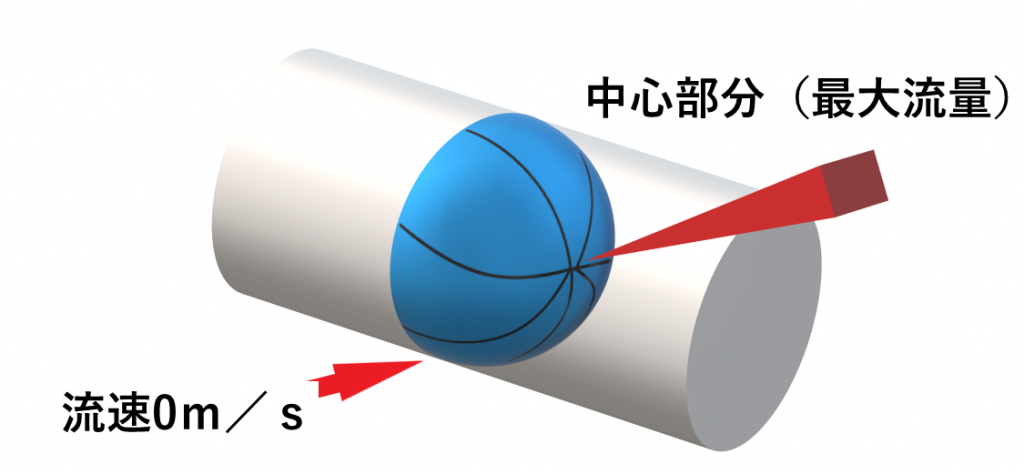
実際は、この内面に接している部分は流速が0(粘性によるもの)で球体状に表した場合を流量で算出しますが、計算では、平均速度として流量を算定していきます。
流量(㎥/s)= 断面積(㎡) × 速度(m/s)
で表します。この中では断面積の口径が変わろうとも、流量は変わりません。
例えば、ホース内径65mmから分岐後、50mmホースへ変わったとしても、総計である流量は変動しないということです。常に流量は一定であり、連続式といいます。
流体エネルギーとベルヌーイの定理

また、消防ポンプでは、圧力を上げることで水にエネルギーを与えることにより、筒先から放水し、飛距離を伸ばしていきます。
この中に流体の持つエネルギーが関係し、主に圧力エネルギー、運動エネルギー重力エネルギーがあります。消防ポンプの圧力操作により、これら3つが相互に変化し、放水量を左右していきます。
まずは理論を理解していきましょう。
圧力エネルギー
例えば、65mmホース内部に水がある場合、この断面積分の水圧を受けながら数メートル移動したときの仕事量を単位J(ジュール)で表すことができます。
これは水圧(Pa)によって移動したこと(m)による仕事量であることから、圧力エネルギーといいます。
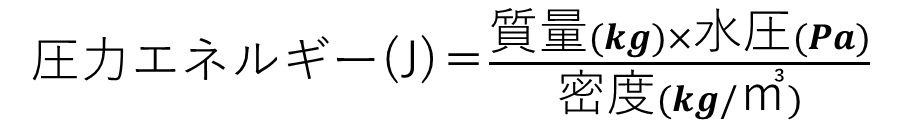
公式ではこのように表せます。移動した距離と断面積が公式にないじゃんと思わるかもしれませんが、変換した結果の式がこのようになります。
変換前:①圧力エネルギー=水圧×断面積×移動した距離
移動した距離は、②質量=密度×断面積×移動した距離で表せます。
②の式を①に代入したときに最初の式になります。興味のある方は変換してみてください。
運動エネルギー
運動エネルギーとは、65mmホース内部の水の重さと流れる量の速さがあるとき、一点の断面積を通る時間を運動エネルギーで表します。
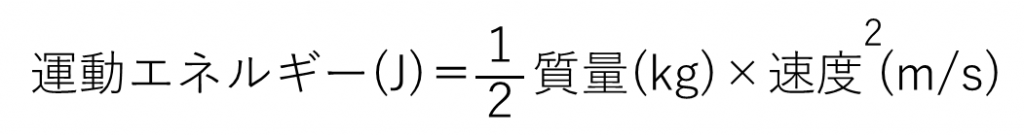
重力による位置エネルギー
位置エネルギーはホース内部の水の重さに掛かる重力と、ポンプ位置からの高さからエネルギーを表します。

ベルヌーイの定理
ベルヌーイの定理はよく聞きますね。これは、流体においてもホースの口径が変わろうが、流速が変わろうが、消防ポンプの圧力が変わろうが、エネルギーの総量は一定を保つ、エネルギー保存の法則が成り立ちます。
それは、このように表せます。単位はJ(ジュール)※Eはエネルギーを表す
圧力E① + 運動E① + 位置E① = 圧力E② + 運動E② + 位置E②
が成り立ちます。
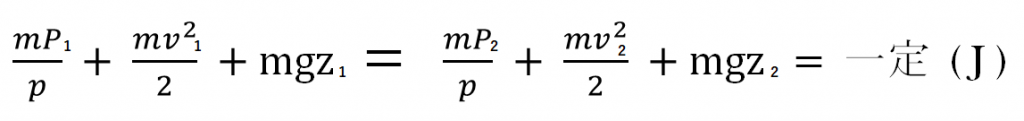
- m:質量(kg)
- P(大文字):圧力(Pa)
- p(小文字):密度(kg/㎥)
- v:速度(v/s)
- g:重力加速度(m/s^2)※s^2の二乗です
- z:高さ(m)
記号で表すとこんな感じです。ちょっと被ってる記号があるので、消しましょう。両辺をm(質量)で割ると
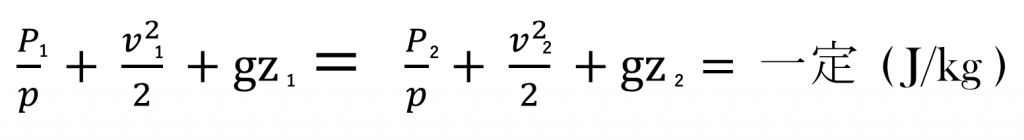
これでも常にエネルギー量は一定です。これをベルヌーイの定理といいます。
エネルギーが常に一定なのは、火災のときでも同じです。どんなエネルギーも何かのエネルギーに変化し、総量は変わらないことは理解しておきましょう。
現時点の単位は(J/kg)となっています。あまり馴染みがない単位なので、分かりやすい単位にしたいと思います。
それは、両辺を重力加速度gで割ると、一定の単位をm(メートル)で表すことができます。
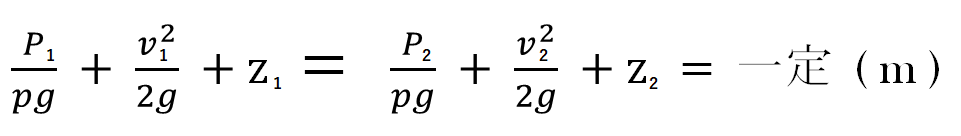
上式の各部分の単位はmとなり、相和もmとなります。左辺の左から圧力ヘッド、速度ヘッド、位置ヘッドといいます。
流体を理論的に考えるとき、分かりやすく変換しているため、よく使う式です。
消防の世界では、これをまんま使うのはスプリンクラーヘッドや屋内消火栓の検査で圧力計算などで活用するときがあります。そのとき、この理論を理解しておけば、配属先が予防課になっても頭には入りやすいでしょう。
消防の活動でこの式を活用することはありません。(笑)
まとめ

- 水の性質を理解する
- 水には僅かな粘性があり、それが摩擦損失を生み出している
- エネルギーには保存の法則があり、常に総量は一定である
- 流体のエネルギー式は活動では覚える必要なし。予防課配属されるならいるよ。
このページをある程度理解できれば、ホースの圧力損失はスッと頭に入りやすいでしょう。
前提知識が合ったうえで勉強していきましょう。











